Error Detection and correction codes | Parity code
An error is the common cause of any system, either it may be digital or analog. Error detection and correction codes allow the detection and correction of an error while transmitting the binary information.
In digital electronics system or digital communication system, the information is transmitted from one system to another system or from one circuit to another in a binary form.
While transmitting the information, an error may occur due to the presence of noise. An error is said to occur, if a signal corresponding to 0 may change to 1 or vice versa.
It is not always possible to avoid those errors, but it is possible to detect and correct the error. First, it is important to detect an error. It is done by adding an extra bit to the transmitted data.
There are different codes like parity code, block parity, hamming code, etc to detect and correct the errors. In this section, you will learn in detail about the parity code.
Parity code
The parity code is used for the purpose of detecting errors during the transmission of binary information. The parity code is a bit that is included with the binary data to be transmitted.
The inclusion of a parity bit will make the number of 1’s either odd or even. Based on the number of 1’s in the transmitted data, the parity code is of two types.
- Even parity code
- Odd parity code
In even parity, the added parity bit will make the total number of 1’s an even number. If the added parity bit make the total number of 1’s as odd number, such parity code is said to be odd parity code.
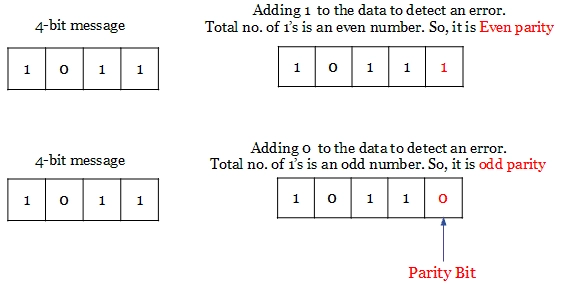
Let us consider the 4-bit message(1011) to be transmitted. Adding 1 to the message will make the total number of 1’s in the message to be an even number. Hence it is called as even parity.
For the same message, adding 0 with the transmitted message will make the total number of 1’s to be an odd number. Hence it is called as odd parity. It is shown in the example below.
The following table shows the some of the 4-bit messages to be transmitted along with the parity bits. The bits in red color are the parity bits.
| 4-bit message | Message with Odd parity | Message with Even Parity |
|---|---|---|
| 0000 | 00001 | 00000 |
| 0001 | 00010 | 00011 |
| 0010 | 00100 | 00101 |
| 0011 | 00111 | 00110 |
| 0100 | 01000 | 01001 |
| 0101 | 01011 | 01010 |
| 0110 | 01101 | 01100 |
| 0111 | 01110 | 01111 |
On the receiver side, if the received data is other than the sent data, then it is an error. If the sent date is even parity code and the received data is odd parity, then there is an error.
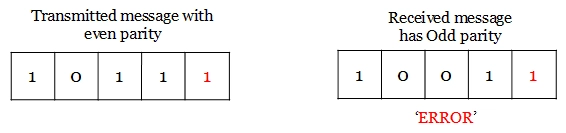
So, both even and odd parity codes are used only for the detection of error and not for the correction in the transmitted data. Even parity is commonly used and it has almost become a convention.
Block Parity
When several binary words are transmitted and received at a time, then such information is regarded as a block of data, having rows and columns. For example, let us consider four eight-bit words, which are to be transmitted, forms a 4 x 8 block. Parity bits are assigned to both rows and columns.
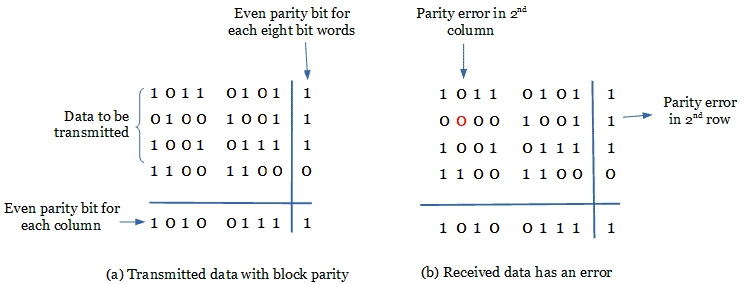
As shown above, even parity is given to each eight-bit word and for each column. In this case, the parity bit is called block parity. The block of data is transmitted from the transmitter side.
Upon analyzing the received block of data(b), the first row has no error as the even parity is maintained. In the second row, the even parity is changed to odd parity. So there is an error in the 2nd row. Even parity is maintained in the third and fourth row and thus, there is no error.
To find out the error bit in the second row, let’s check the column-wise parity. If you do so, in the 2nd column, you can notice the even parity is changed to odd parity. So there is an error in the second column. In all other columns, there is no change in the even parity and hence no error in other columns.
The bit, which is at the intersection of the 2nd row and 2nd column is an error bit. In the above illustration, the error bit is marked in red color. Since the detected error is a single bit, we can change the bit 0 to 1. Thus in block parity, detection and correction of an error are possible with the parity codes.
Now, take a look at the following received message.
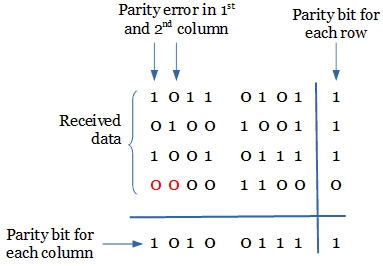
In the above figure, you can observe that there is no parity bit error for each row. But for the 1st and 2nd column the even parity is changed to odd parity, which is an error.
Thus the error is seen in the 1st and 2nd column. In this case, it is possible only to detect the error. It is not possible to correct the error as there is no information revealing the row where the errors occurred.