Phasor diagram of practical transformer on Load

A practical or actual transformer will have winding resistance and leakage reactances both on the primary and secondary sides. When the secondary of the transformer is connected to the load terminals, the transformer is said to be on load. The load can be either resistive, inductive, or capacitive. In this section, let us learn the phasor diagram of practical transformer on load condition.

Let us consider a practical transformer as shown below, which has primary and secondary windings of resistances R₁ and R₂ and reactances X₁ and X₂ respectively.

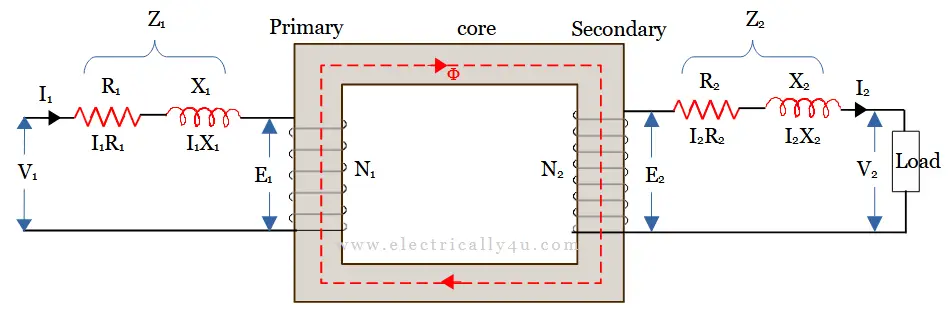
In the above circuit, V₁ and I₁ are the primary voltage and current respectively, E₁ is the induced emf in the primary winding and N₁ is the number of turns in the primary winding. Similarly, N₂ is the number of turns in the secondary winding, E₂ is the induced emf in the secondary winding, V₂ is the terminal voltage and I₂ is the load current in the secondary winding.

The impedance of primary winding and secondary winding is given by,

   

   

Before drawing the phasor diagram of the transformer on load, it is important to learn the operation of transformer on load condition.

Steps to draw the phasor diagram

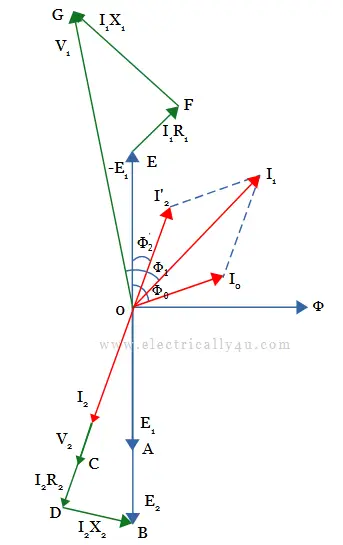
The below diagram shows the phasor diagram of the transformer on resistive load. Follow the below procedure to draw the diagram.

• Consider the flux Φ as the reference phasor.
• The EMF induced in the transformer E₁ is drawn lagging the flux(Φ) by 90⁰ as OA.
• The counter-induced emf(-E₁) in the primary winding is drawn equal and opposite to E₁.
• Due to winding resistance and leakage reactance, the secondary current I₂ lags behind the induced emf E₂ and is drawn as OI₂.
• Since the load is resistive, secondary voltage V₂ is drawn in phase with I₂ as OC.
• The voltage drops due to winding resistance(I₂R₂) in the secondary is drawn parallel to the secondary current phasor I₂ from V₂ phasor as CD = I₂R₂.
• Similarly, the voltage drop due to reactance(I₂X₂) in the secondary winding is drawn perpendicular to the current phasor I₂ from D as DB = I₂X₂.
• Now, the phasor sum of terminal voltage V₂, voltage drop due to secondary resistance I₂R₂, and voltage drop due to secondary reactance I₂X₂ is equal to induced emf E₂ in the secondary winding. Its magnitude is expressed as,

     
• The current in the primary winding has two components: no-load current(I₀) and load component of the primary current(I₂‘).
• Draw the no-load current I₀ by lagging -E1 by no-load angle Φ₀.
• Since I₂‘ is the load component of the primary current, it is drawn equal and opposite to I₂.
• The phasor sum of I₀ and I₂‘ gives the primary current I₁.
• The voltage drops due to winding resistance(I₁R₁) in the primary is drawn parallel to the primary current phasor I₁ from -E₁ phasor as EF = I₁R₁.
• Similarly, the voltage drop due to reactance(I₁X₁) in the primary winding is drawn perpendicular to the current phasor I₁ from D as FG = I₁X₁.
• Now, the phasor sum of counter-induced emf -E₁, voltage drop due to primary resistance I₁R₁, and voltage drop due to primary reactance I₁X₁ gives the applied voltage V₁ to the primary winding. Its magnitude is expressed as,

     

• The phase angle Φ₁ between V₁ and I₁ gives the power factor angle of the transformer.

The same procedure is repeated for inductive load and capacitive load. However, in the case of inductive load, secondary voltage V₂ is drawn leading the secondary current I₂ by an angle Φ₂ as OC. In the case of capacitive load, secondary voltage V₂ is drawn lagging the secondary current I₂ by an angle Φ₂ as OC.

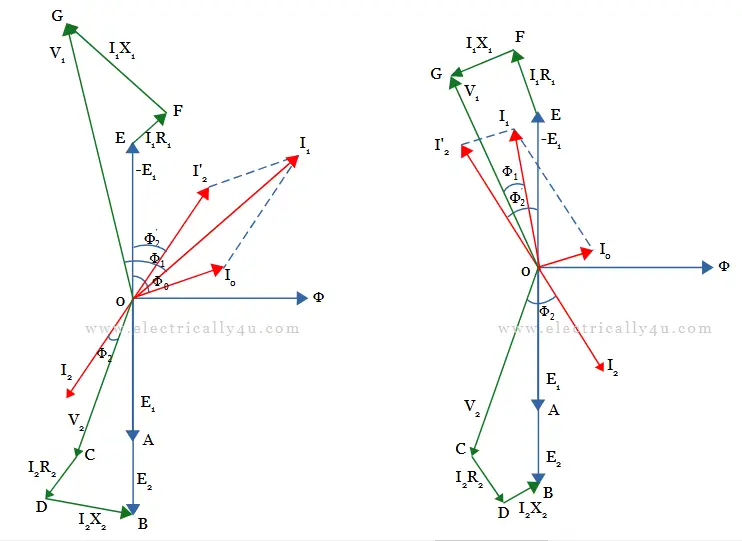
From the phasor diagrams, the following equations can be derived.

(a) For pure resistive load,

   

   

   

Using the transformation ratio,

   

(b) For resistive-inductive load,

   

   

   

   

(b) For resistive-capacitive load,