Star Delta Transformation with solved problems
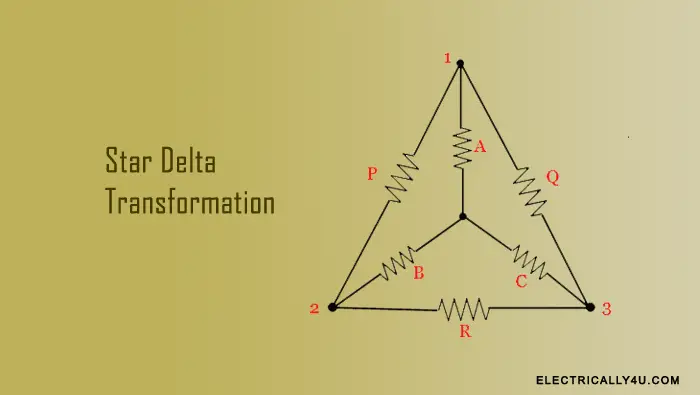
Star delta transformation is a simple and useful technique used for solving complex networks. The three circuit elements, such as resistance, inductance, and capacitance, can be connected and represented in two different ways.
- Star (Y) connection
- Delta (Δ) connection
In a star connection, the branches containing the circuit elements are connected to a common point, creating a Y shape structure, hence called a Wye connection. Whereas in a delta connection, the branches are connected to form a closed triangular loop connected end to end.
It can be easily transformed from one connection to another using star delta transformation and delta star transformation. This transformation technique helps to reduce the mathematical complexity involved in solving a circuit.
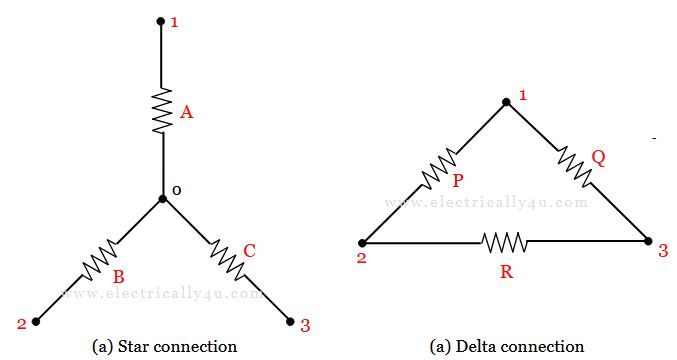
In the above circuits, if the resistances across the terminals 12, 23 and 31 are equal, then they are said to be equal circuits.
Delta star transformation
In the star-connected circuit, the resistances across the terminals 12, 23 and 31 can be written as,
![\[R_{12} = A + B --->(1) \]](https://electrically4u.com/wp-content/ql-cache/quicklatex.com-5bc974cc83868486026701ae58f4a44a_l3.png "Rendered by QuickLaTeX.com")
![\[R_{23} = B + C --->(2) \]](https://electrically4u.com/wp-content/ql-cache/quicklatex.com-8eb3af0debec92447d992493c9cd3bde_l3.png "Rendered by QuickLaTeX.com")
![\[R_{31} = C + A --->(3) \]](https://electrically4u.com/wp-content/ql-cache/quicklatex.com-a98d4c549ab71420fe8bf801e8193893_l3.png "Rendered by QuickLaTeX.com")
Similarly in the delta connected circuit, the resistances across the terminals 12, 23 and 31 can be written as,
![\[R_{12} =P || (Q + R) = \frac{P (Q + R)}{P + Q + R}} --->(4) \]](https://electrically4u.com/wp-content/ql-cache/quicklatex.com-091b4f788e6cb47df622ca5c289b35f2_l3.png "Rendered by QuickLaTeX.com")
![\[R_{23} =R || (P + Q) = \frac{R (P + Q)}{P + Q + R}} --->(5) \]](https://electrically4u.com/wp-content/ql-cache/quicklatex.com-1e321f0a02b44bd9e0aadb97051cea60_l3.png "Rendered by QuickLaTeX.com")
![\[R_{31} =Q || (P + R) = \frac{Q (P + R)}{P + Q + R}} --->(6)\]](https://electrically4u.com/wp-content/ql-cache/quicklatex.com-f1386839fb725c51af7cfe2ae0860807_l3.png "Rendered by QuickLaTeX.com")
Now, for the two circuits to be equal, the resistances of star and delta circuits must be equal. Thus equating (1), (2) and (3) with (4), (5) and (6), respectively, we get
![\[ A + B = \frac{P (Q + R)}{P + Q + R}} --->(7) \]](https://electrically4u.com/wp-content/ql-cache/quicklatex.com-1adeaf5245bab1c2357706c37c3f1ebe_l3.png "Rendered by QuickLaTeX.com")
![\[B + C = \frac{R (P + Q)}{P + Q + R}} --->(8) \]](https://electrically4u.com/wp-content/ql-cache/quicklatex.com-b486a2b35c973f72b6c12f5c357dea12_l3.png "Rendered by QuickLaTeX.com")
![\[C + A = \frac{Q (P + R)}{P + Q + R}} --->(9) \]](https://electrically4u.com/wp-content/ql-cache/quicklatex.com-38603e9cd581d71ec6eb4565107c991b_l3.png "Rendered by QuickLaTeX.com")
Adding the equations (7), (8) and (9), we get
![\[ A + B + B + C + C + A = \frac{PQ + PR + PR + QR + PQ + QR}{P + Q + R} \]](https://electrically4u.com/wp-content/ql-cache/quicklatex.com-359e17ca602339b41d4ed46da79cb418_l3.png "Rendered by QuickLaTeX.com")
![\[ 2(A + B + C) = \frac{ 2(PQ + PR + QR) }{P + Q + R} \]](https://electrically4u.com/wp-content/ql-cache/quicklatex.com-ad8324b6d2fd8c3dddadc3e7d693340d_l3.png "Rendered by QuickLaTeX.com")
![\[ A + B + C = \frac{PQ + PR + QR}{P + Q + R} --->(10) \]](https://electrically4u.com/wp-content/ql-cache/quicklatex.com-e0d4716c3b976416f12e364b90280cb0_l3.png "Rendered by QuickLaTeX.com")
Now subtracting equations (7), (8) and (9) from (10), we get
![\[ C = \frac{QR}{P + Q + R} --->(11) \]](https://electrically4u.com/wp-content/ql-cache/quicklatex.com-d191bd4b724ba27f9f979c1040d418b8_l3.png "Rendered by QuickLaTeX.com")
![\[ A = \frac{PQ}{P + Q + R} --->(12) \]](https://electrically4u.com/wp-content/ql-cache/quicklatex.com-d18b533813be0d2e3ef3c9379b278eba_l3.png "Rendered by QuickLaTeX.com")
![\[ B = \frac{PR}{P + Q + R} --->(13) \]](https://electrically4u.com/wp-content/ql-cache/quicklatex.com-0d5ca83522e0ee7dd7eadb012a3a7da6_l3.png "Rendered by QuickLaTeX.com")
Using the above equations (11), (12), and (13), a delta connection with resistances P, Q, and R can be converted to a star connection with resistances A, B, and C. The equivalent star resistance connected across the given terminal is equal to the product of the two delta resistances connected to the same terminal divided by the sum of the delta-connected resistances.
If all three resistances in the delta connection are same (i.e. P = Q = R), then the equivalent star resistance can be derived considering any one of the equations from (11) to (13). Here, from equation (11),
![\[ C = \frac{R.R}{R + R + R} = \frac{R^2}{3R} = \frac{R}{3}\]](https://electrically4u.com/wp-content/ql-cache/quicklatex.com-7ff9102fa2d05de151e9e389045c6e74_l3.png "Rendered by QuickLaTeX.com")
It means the star-connected resistance (C) is 1/3 times delta connected resistance (R).
Star delta transformation
For the star to delta transformation, multiply equations (11) & (12), (12) & (13), (13) & (11), and adding those, we get
![\[ CA + AB + BC = \frac{Q^{2}PR + P^{2}QR + R^{2}PQ}{(P + Q + R)^{2}}\]](https://electrically4u.com/wp-content/ql-cache/quicklatex.com-adc216bcf7fcd3466ac7f86c6409ad0b_l3.png "Rendered by QuickLaTeX.com")
![\[ AB + BC + CA = \frac{P.Q.R (Q + P + R)}{(P + Q + R)^{2}} \]](https://electrically4u.com/wp-content/ql-cache/quicklatex.com-002fc41468898633878eef6b99796b14_l3.png "Rendered by QuickLaTeX.com")
![\[ AB + BC + CA = \frac{P.Q.R}{P + Q + R} --->(14) \]](https://electrically4u.com/wp-content/ql-cache/quicklatex.com-2a09d8044a848fffafea6b19d70ee76c_l3.png "Rendered by QuickLaTeX.com")
Now dividing the equation (14) by (11), we get,
![\[ \frac{AB + BC + CA}{C} = \frac{P.Q.R}{(P + Q + R)} \times \frac{(P + Q + R)}{QR} \]](https://electrically4u.com/wp-content/ql-cache/quicklatex.com-f3b5808791086d4bcf314d4e2e608fff_l3.png "Rendered by QuickLaTeX.com")
![\[ \frac{AB + BC + CA}{C} = P \]](https://electrically4u.com/wp-content/ql-cache/quicklatex.com-3d1c340470757b7f2b1fee9d7ba1eae3_l3.png "Rendered by QuickLaTeX.com")
![\[ P = \frac{AB + BC + CA}{C} --->(15) \]](https://electrically4u.com/wp-content/ql-cache/quicklatex.com-2406b0fe02c5afcccd9ac69f99260607_l3.png "Rendered by QuickLaTeX.com")
Similarly, dividing equation (14) by (12) and (13) separately, we get,
![\[ Q = \frac{AB + BC + CA}{B} --->(16) \]](https://electrically4u.com/wp-content/ql-cache/quicklatex.com-4fdec0e306af6a7859832b9f990b773e_l3.png "Rendered by QuickLaTeX.com")
![\[ R = \frac{AB + BC + CA}{A} --->(17) \]](https://electrically4u.com/wp-content/ql-cache/quicklatex.com-6bc17ed15c7f7bdcdae517d5eaa6e35d_l3.png "Rendered by QuickLaTeX.com")
Using the above equations (15), (16), and (17), a star connection with resistances A, B, and C can be converted to a delta connection with resistances P, Q, and R. The equivalent delta resistance connected across the given terminal is equal to the sum of the products of all possible pairs of star resistances divided by the opposite resistance of the star circuit.
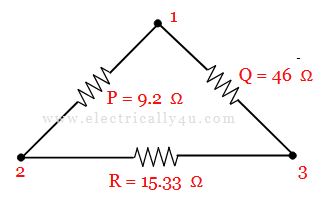
Solved Problem 1
For the given delta connected circuit, obtain the star connected circuit.
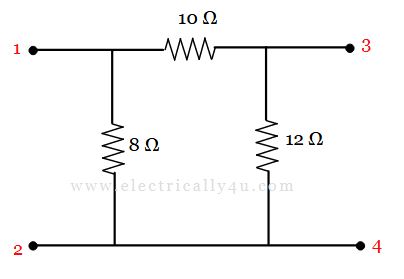
The given circuit is called pi connection or delta connection. It can be modified as it to look exactly like a delta connection.
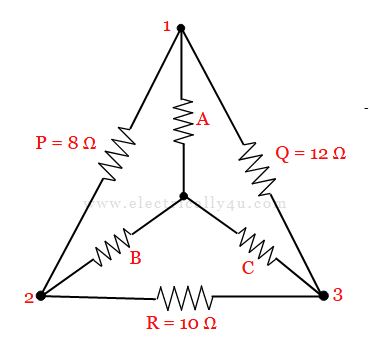
Now, using the formulas for delta star transformation,
![\[ A = \frac{PQ}{P + Q + R} = \frac{8 \times 12}{8 + 10 + 12} = 3.2 \Omega \]](https://electrically4u.com/wp-content/ql-cache/quicklatex.com-01b0cd6d058bf0625aa91228348124f9_l3.png "Rendered by QuickLaTeX.com")
![\[ B = \frac{PR}{P + Q + R} = \frac{8 \times 10}{8 + 10 + 12} = 2.67 \Omega \]](https://electrically4u.com/wp-content/ql-cache/quicklatex.com-176fd5806c28c6ecc55f4a757eaac49f_l3.png "Rendered by QuickLaTeX.com")
![\[ C = \frac{QR}{P + Q + R} = \frac{12 \times 10}{8 + 10 + 12} = 4 \Omega \]](https://electrically4u.com/wp-content/ql-cache/quicklatex.com-00dc032fac45941ed711a51762ccdeed_l3.png "Rendered by QuickLaTeX.com")
The obtain star connected circuit is drawn below,
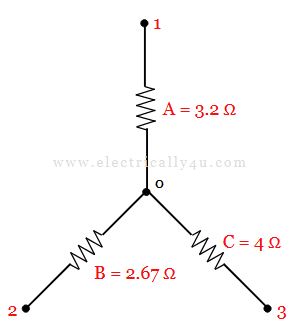
Solved Problem 2
Convert the given star connected circuit to delta connected circuit.
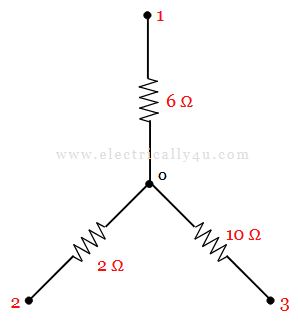
Now, using the formulas for star delta transformation,
![\[ P = \frac{AB + BC + CA}{C} = \frac{(6\times 2)+(2\times 10)+(10\times 6)}{10} = 9.2 \Omega \]](https://electrically4u.com/wp-content/ql-cache/quicklatex.com-9e3eeb40343d57497ca0bda268d7d85a_l3.png "Rendered by QuickLaTeX.com")
![\[ Q = \frac{AB + BC + CA}{B}= \frac{(6\times 2)+(2\times 10)+(10\times 6)}{2} = 46 \Omega \]](https://electrically4u.com/wp-content/ql-cache/quicklatex.com-64ad746a117bbe95a547791cbd0e6e2c_l3.png "Rendered by QuickLaTeX.com")
![\[ R = \frac{AB + BC + CA}{A} = \frac{(6\times 2)+(2\times 10)+(10\times 6)}{6} = 15.33 \Omega\]](https://electrically4u.com/wp-content/ql-cache/quicklatex.com-70cbad8cb6b8241073d20e445f8a48fe_l3.png "Rendered by QuickLaTeX.com")
Thus the delta circuit is drawn as below,
